[Algorithm] Recursive Call

재귀함수란

함수안에서 자기 자신을 부르는 함수 호출을 재귀함수 (recursive call) 이라고 부른다. 재귀호출은 일반적인 개발을 할 때 잘 사용하지 않지만, 알고리즘을 구현할 때 매우 유용하게 사용된다. 보통 일반적으로 사용하는 반복문을 통해 구현하는 것 보다 재귀호출을 이용해 구현한 코드가 좀 더 직관적이고 이해하기 쉽다. 재귀함수를 가장 잘 표현한 그림이 있어 가져왔다. 그림은 펜네 블로그 에서 참조하였으며, 재귀 함수에 대한 설명도 잘되어있으니 한번 들어가보길 바란다.

재귀함수 표현 그림

위의 그림을 보면 정확하게 이해할 수 있다. 끝이 없이 자기자신을 부를 수 있다. 너무 좋지 않나? 하지만 이게 재귀함수의 단점이다. 컴퓨터는 메모리라는 자원을 가지고 있다. 메모리라는 자원을 쪼개서 프로그램들이 공유해서 사용한다. (이 부분을 자세히 알고 싶다면 운영체제의 메모리 부분을 참고해보기 바란다.) 우선 그 쪼개진 자원을 쉽게 설명하기 위해 frame이라고 하자. 그렇다면 메모리는 다수의 frame이라고 볼 수 있다. 재귀 함수를 호출 할 때마다 하나의 frame이 생기게 되는데 무한적으로 호출하게 된다면 결국 메모리의 frame을 다 사용하게 된다. 이 경우를 stack overflow 라고 한다. 즉, frame이 넘치는 것이라고 생각하면 쉽다. 왜 stack 구조로 되있는가? 라고 한다면, 함수의 callee covention 부분을 참고하기 바란다. 이 부분에서 다 설명하기에는 너무 많은 내용을 필요로 한다 ㅠㅠ,, 시간이 되면 추가 포스팅을 작성하도록 하겠다. 여기서는 frame 넘친다면 stack overflow라고 하는구나 그리고 재귀함수는 무한정 호출하게 된다면 stack overflow가 발생하는구나 정도만 기억하도록 하자!

재귀함수의 간단한 예시

우리는 컴퓨터를 하는 사람이다. 코딩을 하는 프로그래머이다. 역시 소스코드를 통해 이해하는 것이 빠를 것이다. 간단한 재귀함수의 예시를 통해 알아보자.

위의 예시는 코딩 도장 에서 발췌하였다.

#include <cstdio>

void hello()
{
    printf("Hello, world!\n");

    hello();    // hello 함수 안에서 hello 함수 호출
}

int main()
{
    hello();    // hello 함수 최초 호출

    return 0;
}

위의 코드를 보자. main()에서 hello() 라는 함수를 호출한다. hello()를 보자면 내부적으로 hello world를 출력하고 또!! hello()를 호출한다. 또다시 hello()함수가 호출되고 hello() 내에서는 hello world를 출력하게 되고 hello()를 호출한다. 이 동작이 무한정 반복되게 되는데.. 그럴경우 Stack overflow가 발생하게 된다. 그림을 보자.

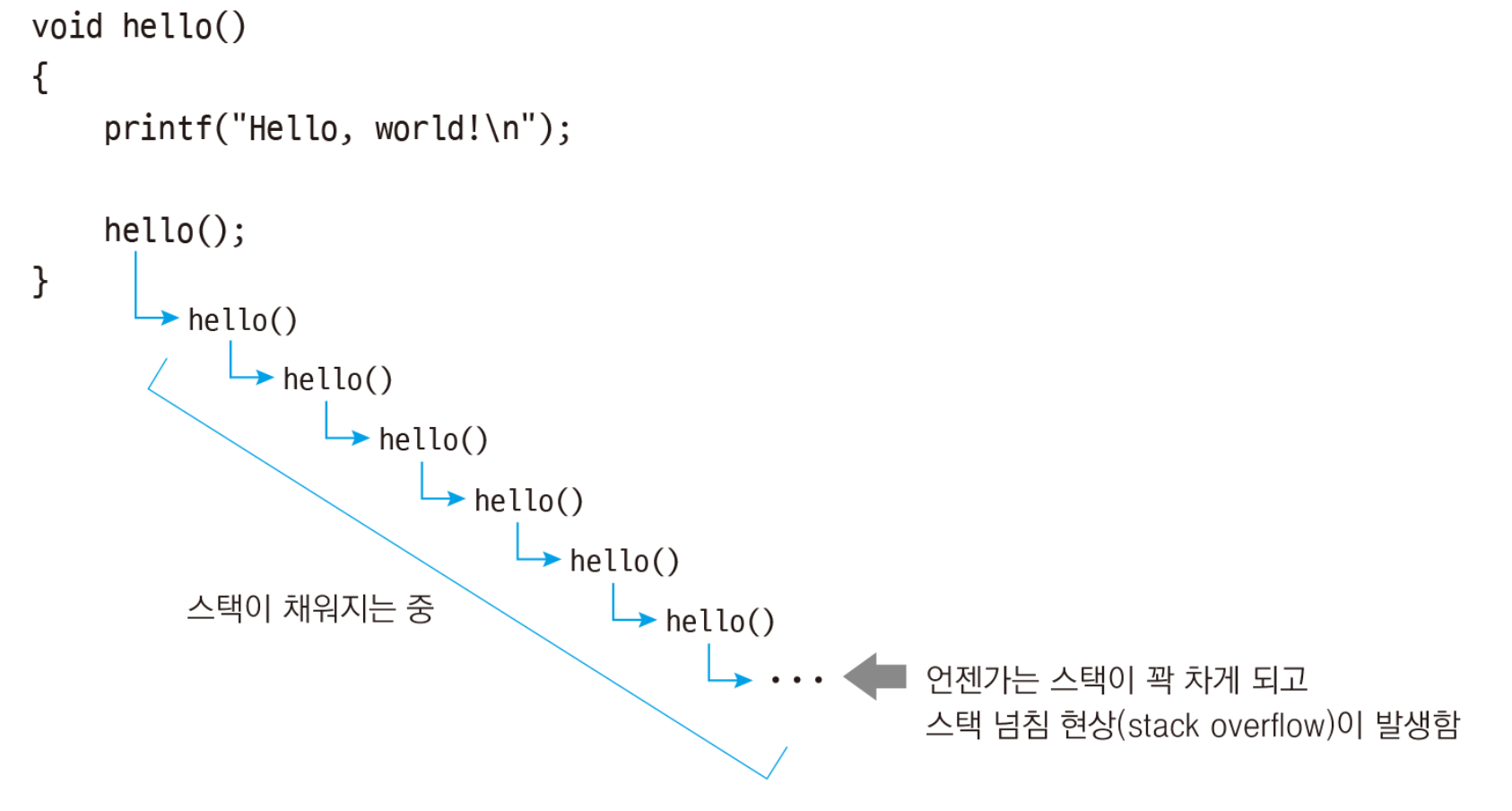
hello 함수 호출과정

위의 그림을 보면 정확하게 이해할 수 있다.

재귀함수의 골치덩어리인 stack overflow를 해결하기 위해서는 꼭 종료함수를 만들어주어야한다.

기억하자! 종료함수 즉, 탈출조건을 항상 고려해야한다.

#include <iostream>

using namespace std;

void hello(int cnt)
{
	if (cnt == 3) {
		cout << "hello world..!" << endl;
		return;
	}

	cout << "cnt is " << cnt << endl;
	hello(cnt + 1);
}

int main()
{
	hello(0);
}

위의 코드의 결과를 보자.

output
cnt is 0
cnt is 1
cnt is 2
hello world..!

위의 코드의 핵심 포인트는 hello 함수 내 탈출조건인 if문이다. 어떤 기준이 된다면 이제 돌아가겠다 하는 것이다.

재귀 원리

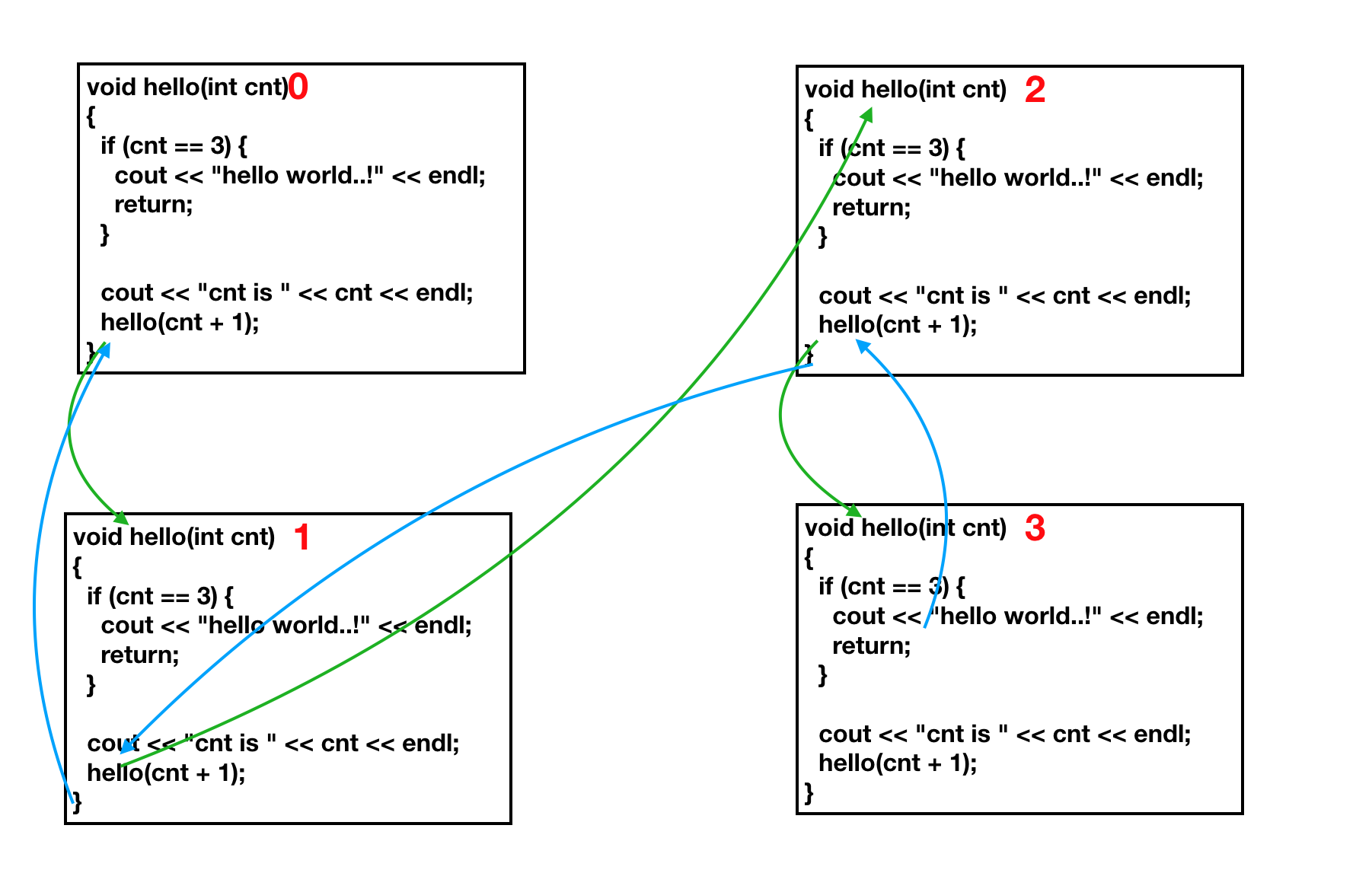
위의 그림을 보자. 위의 그림이 난잡할 수 있지만, 초록색은 호출하는 함수이고 파란색은 복귀하는 함수 숫자는 초록색으로 호출 할때 변화되는 것이다. 그림을 따라 가면서 출력된 결과값을 보자. 충분히 이해할 수 있을 것이라 생각한다. (그림은 내가 그린 거라 복잡할 수도 있지만.. 코딩도장에 좀 더 간단하게 나와있으니 거길 참고해도 된다.)

재귀함수의 장점

재귀 함수의 단점은 메모리의 용량을 초과하는 stack overflow가 발생하는것으로 명확하다. 그렇다면 장점은 뭘까..? 재귀함수의 장점은 크게 두가지이다.

알고리즘 자체가 재귀적으로 표현이 자연스러울 경우 가독성이 좋아짐 (e.g. tree, quick sort, permutation 등)
변수 사용을 줄여줌

첫 번째 장점 같은 경우 쉽게 알 수 있다. 위의 간단한 예제만 보더라도 좀 더 깔끔하게 소스코드를 구축할 수 있다. 조금 더 복잡한 예시를 보자.

/* low  --> Starting index,  high  --> Ending index */
quickSort(arr[], low, high)
{
    if (low < high)
    {
        /* pi is partitioning index, arr[pi] is now
           at right place */
        pi = partition(arr, low, high);

        quickSort(arr, low, pi - 1);  // Before pi
        quickSort(arr, pi + 1, high); // After pi
    }
}

위의 코드는 Quick sort 예시 이다. 만약 재귀가 아니라면 엄청난 loop들이 들어가게 될 것이며 해석이 어려울 것이다. 위의 함수를 보자면, 재귀함수로 인해 argument에 따라 글을 읽듯이 해석하면 된다.

두 번째 장점은 변수사용을 줄여주는 것이다. 변수사용을 줄여주는 것을 좀 더 추상적으로 이야기하자면, mutable state를 취할 수 있는 상황을 줄여준다. 결과적으로, 프로그램에서 오류가 발생할 수 있는 가능성 즉, 잘못된 state가 전달될 가능성을 줄여주고 증명을 하기가 쉬워진다는 장점이 있다.

프로그램이 복잡해지면 복잡해질수록 mutable state를 가능한 피하는 것이 프로그램을 작성하는데 중요한 원칙이 될 수 밖에 없다. mutable state를 가능한 한 피하는 것은 변수의 수를 줄이는 것과 변수가 가질 수 있는 값의 종류 또는 범위를 정확히 제한할 수 있다.

간단한 예시를 보자.

program 1.

int sum = 0;
for(int i = 0; i <= 100; ++i) {
sum += i;
}
cout << sum << endl;

program 2.

int sum(const int x, const int acc) {
if(x > 100) return acc;
else return sum(x + 1, x + acc);
}

cout << sum(0, 0) << endl;

위의 코드를 보자. program1은 변수를 2개 사용하고 있으며, program2는 변수를 하나도 사용하고 있지 않다. program2에서 사용하는 x, acc는 const 상수이다. 즉, 변수가 없다는 것을 알 수 있다. 이런 프로그램을 작성할 경우 추후 sum을 다른 함수에서 사용하거나 다른 곳에서 증가시킬 수 있는 상황을 고려할 필요가 없어진다. 즉, mutable state 가 줄어드는 것이다.

재귀함수 예시

재귀 함수의 예시를 보자. 예시는 너무 많다. 하지만 생각해보면서 풀기 좋은 문제를 예시로 가져왔다.

순열은 고등학교 시절에 많이 배웠던 것이다. 몰라도 괜찮다. 인터넷에 너무 잘나와있다. 순열이란 서로 다른 개의 원소에서 개를 뽑아 한 줄로 세우는 경우의 수이다. 예를들어 서로다른 색상의 공이 들어있는 주머니에서 공을 뽑아 한줄로 세우는 것이라 생각하면 된다. 순열에는 두가지 방법이 있는데, 공을 중복으로 뽑을 수 있느냐 아니냐로 나뉜다.

중복 순열

중복 순열이란 중복으로 수를 뽑을 수 있는 순열을 말한다. 즉, 주머니에 공이 들어있는데 한 숫자를 뽑고 다시 주머니에 넣는다고 생각하면된다. 예를 들어 1, 2, 3이라는 숫자가 주머니에 들어가 있다고 치자. 그럴경우 1, 1, 1 이라는 수를 뽑을 수 있는 케이스가 존재하는 순열을 중복순열이라고 한다.

#include <iostream>
#define MAX 10
using namespace std;

int arr[MAX];

void perm (int idx, int cnt)
{
	if (idx == cnt) {
		for (int i = 0; i < cnt; i++) {
			cout << arr[i] << " ";
		}
		cout << endl;
		return;
	}

	for (int j = 0 ; j < cnt; j++) {
			arr[idx] = j + 1;
			perm(idx + 1, cnt);
	}
}

int main() {
	perm(0, 3);
}

위의 소스코드를 보면, 탈출 조건이 존재한다는 것을 알 수 있다. 탈출 조건이 있어야 stack overflow가 발생하지 않는다는 것을 한번더 상기시키자. 인자로 전달되는 idx를 주목해서 보자!

중복된 수가 없는 순열

#include <iostream>
#define MAX 10
using namespace std;

int arr[MAX];
bool visited[MAX];
void perm (int idx, int cnt)
{
  if (idx == cnt) {
    for (int i = 0; i < cnt; i++) {
      cout << arr[i] << " ";
    }
    cout << endl;
    return;
  }

  for (int j = 0 ; j < cnt; j++) {
      if (!visited[j]) {
      arr[idx] = j + 1;
      visited[j] = true;
      perm(idx + 1, cnt);
      visited[j] = false;
    }
  }
}

int main() {
  perm(0, 3);
}

위의 코드는 중복 없이 순열을 출력하는 코드이다. 해당코드에서 핵심은 visited 배열 이다. visited 배열을 통해 방문유무를 체크해야한다. for문을 돌면서 첫 번째 공간은 방문했다 체크를하고 recursive 함수를 호출해야한다. 이 부분은 BOJ 문제를 통해 좀 더 자세하게 설명하도록 한다.